Exploring a shipping puzzle

← Back to Kevin's homepagePublished: 2018 October 23Last updated: 2018 November 7

A friend recently told me about a puzzle, which is a great excuse to explore programming craft.

This article outlines my approaches to solving the puzzle:

Update: See part 2 for more solutions (and proofs!)

The shipping puzzle

Here’s the puzzle: Given a set of “legs”, each consisting of a day of the week, origin and destination:

M PDX SEA
T PDX SFO
T SEA DEN
W DEN PDX
R PDX DEN
F DEN JFK

How can the legs be partitioned into “routes” for individual airplanes, subject to the following constraints:

A trivial solution meeting these constraints would be to consider each leg as a separate route — but that would require a lot of planes. The puzzle is to find a partitioning with the fewest possible routes.

In this example, we know we need at least two routes, since there are two legs scheduled on Tuesday. One possible solution is for one plane to fly PDX, SEA, DEN, PDX, DEN, JFK and a second plane to fly just the Tuesday PDX to SFO leg.

If you want to try your hand at this puzzle yourself, you can try this 10,000 leg data set.

First, try the simplest thing that could work

When I first encounter a new problem, I try to wrap my head around it by first trying the simplest thing that could work. This helps me get a handle on the problem, and lets me test my understanding of the fundamentals before I start to worry about things like the efficiency of the calculation, optimality of the solution, etc.

I started with Clojure, since that language makes it easy to interactively “sketch” with little bits of code.

The first thing I did was parse the input data into a data structure that modeled the domain: An unordered set of maps, with each map corresponding to a leg:

(def legs
  (->> (str/split (slurp "legs.txt") #"\n")
       (map (fn [s]
              (let [[id start end dow] (str/split s #"\s+")]
                {:id id :start start :end end :dow dow})))
       set))

The simplest way I could think of to find a partitioning (not necessarily an optimal one) was to consider the legs on each day of the week, starting with Monday. On Monday, no routes will be in progress, so we’ll need to create a new route (that is, assign a new plane) for each Monday leg.

Then we look at all of the Tuesday legs and either:

Then we repeat this for each day of the week.

Since we’re going through all of the legs and assigning that leg to a route, we know we’ll use them all up. (We don’t know if this algorithm is optimal or fast, but it should be correct.)

Here’s my first pass:

(def tomorrow
  {"M" "T", "T" "W", "W" "R", "R" "F"})

(defn add-legs
  [dow possible-legs routes]
  (reduce (fn [routes {:keys [start] :as l}]
            (if-let [r (->> routes
                            (filter #(let [last-leg (last %)]
                                       (and (= dow (tomorrow (:dow last-leg)))
                                            (= start (:end last-leg)))))
                            first)]
              (-> routes
                  (disj r)
                  (conj (conj r l)))
              (conj routes [l])))
          routes possible-legs))

(defn attempt-1
  [legs]
  (let [dow-legs (group-by :dow legs)]
    (->> #{}
         (add-legs "M" (dow-legs "M"))
         (add-legs "T" (dow-legs "T"))
         (add-legs "W" (dow-legs "W"))
         (add-legs "R" (dow-legs "R"))
         (add-legs "F" (dow-legs "F")))))

On the 10,000 leg data set, this code finds 2414 routes in 5.00 ± 0.04 seconds. (I’m on a 1.7 GHz Macbook Air from 2013.)

Notes about this first pass:

Again, I didn’t expect this algorithm to be optimal (to partition with the minimal number of routes). To get a rough sense of the “optimality”, I updated the algorithm to randomly choose between the available legs (i.e., within the reducing function I replaced first with a nil-punning rand-nth). Then each run of the function will likely yield a different legal partitioning.

Interestingly, the dozen solutions I “sampled” in this way all had the same number of routes. This doesn’t mean it’s optimal, but it’s suggestive.

Second pass: Performance

For the second pass, I punted again on the optimality question in favor of writing a faster implementation of the same algorithm.

The two optimizations are to:

The outer loop goes through the days of the week, and the inner loop goes thorough the available legs for that day of the week.

(defn attempt-2
  [legs]
  (let [dow-legs (group-by :dow legs)]
    (loop [[dow & dows] ["M" "T" "W" "R" "F"]
           routes-by-position {}
           finished-routes #{}]

      (if (nil? dow)
        ;;done
        (reduce into finished-routes (vals routes-by-position))

        ;;else get all of today's legs and try to attach to routes
        (let [[extended-routes-by-position unextended-routes-by-position]
              (loop [[l & ls] (dow-legs dow)
                     extended-routes-by-position {}
                     unextended-routes-by-position routes-by-position]
                (if (nil? l)
                  [extended-routes-by-position unextended-routes-by-position]
                  (if-let [r (-> unextended-routes-by-position
                                 (get (:start l))
                                 first)]

                    ;;Add this leg to a route
                    (recur ls
                           (update extended-routes-by-position (:end l) conj (conj r l))
                           (update unextended-routes-by-position (:start l) rest))

                    ;;Leg can't be added to existing route, start a new one
                    (recur ls
                           (update extended-routes-by-position (:end l) conj [l])
                           unextended-routes-by-position))))]

          (recur dows
                 ;;extended routes can keep being extended
                 extended-routes-by-position
                 ;;routes that weren't extended today must be finished; move them out so they won't slow down future calcs
                 (reduce into finished-routes (vals unextended-routes-by-position))))))))

This solution also finds 2414 routes, but in just 23 ± 1 ms (about a thousandth the time of the first solution). Not bad.

Things to note:

Third pass: Alloy model

For fun, I thought I’d also solve the problem with Alloy, a verification tool based on first order relational logic.

abstract sig DoW {
  tomorrow: lone DoW
}

one sig M, T, W, R, F extends DoW {}
fact { tomorrow = M->T + T->W + W->R + R->F }

abstract sig Leg {
  start: String,
  end: String,
  dow: DoW,
}

sig Route {
  legs: seq Leg,
}

fact {
  // routes can't have duplicate legs
  all r: Route | not r.legs.hasDups

  // legs must follow each other in time and space
  all r: Route | 
    all l, l': r.legs.elems |
      (plus[r.legs.idxOf[l], 1] = r.legs.idxOf[l']) => {
        l'.start = l.end
        l'.dow = l.dow.tomorrow
      }

  // no sharing legs
  all disj r, r': Route | no (r.legs.elems & r'.legs.elems)

  // all legs must be consumed by the routes
  Leg = Route.legs.elems

}

run show {}

One fun aspect of Alloy is that it isn’t like a typical programming language that merely processes some provided data. Rather, Alloy will generate instances of data that conform to the constraints that you give it.

So if we just tell Alloy about the names of cities:

fact cityNames {
  Leg.start + Leg.end = "PDX" + "DEN" + "SEA" + "SFO" + "JFK"
}

it can generate instances from that, and even present them to you visually:

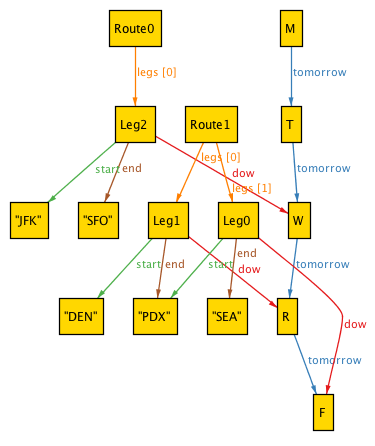
Alloy instance graph

This is a bit clearer to read as an Alloy relational table:

┌──────────┬──────┐ ┌────────┬─────┬─────┬───┐ ┌────────┬────────┐
│this/Route│legs  │ │this/Leg│start│end  │dow│ │this/DoW│tomorrow│
├──────────┼─┬────┤ ├────────┼─────┼─────┼───┤ ├────────┼────────┤
│Route⁰    │0│Leg²│ │Leg⁰    │"PDX"│"SEA"│F⁰ │ │F⁰      │        │
├──────────┼─┼────┤ ├────────┼─────┼─────┼───┤ ├────────┼────────┤
│Route¹    │0│Leg¹│ │Leg¹    │"DEN"│"PDX"│R⁰ │ │M⁰      │T⁰      │
│          ├─┼────┤ ├────────┼─────┼─────┼───┤ ├────────┼────────┤
│          │1│Leg⁰│ │Leg²    │"JFK"│"SFO"│W⁰ │ │R⁰      │F⁰      │
└──────────┴─┴────┘ └────────┴─────┴─────┴───┘ ├────────┼────────┤
                                               │T⁰      │W⁰      │
                                               ├────────┼────────┤
                                               │W⁰      │R⁰      │
                                               └────────┴────────┘

Here Alloy has generated two routes (a Wednesday JFK->SFO route and a Thursday/Friday DEN->PDX->SEA route) that satisfy the general constraints of the problem, as well as the cityNames constraint that those cities must all appear.

Alloy doesn’t actually have facilities for reading files or parsing strings, so to solve the actual puzzle I “imported” the data by writing a Clojure program to generate constraints as Alloy source code:

one sig L1 extends Leg {} { dow = M && start = "PDX" && end = "SEA" }
one sig L2 extends Leg {} { dow = T && start = "PDX" && end = "SFO" }
one sig L3 extends Leg {} { dow = T && start = "SEA" && end = "DEN" }
one sig L4 extends Leg {} { dow = R && start = "PDX" && end = "DEN" }
one sig L5 extends Leg {} { dow = W && start = "DEN" && end = "PDX" }
one sig L6 extends Leg {} { dow = F && start = "DEN" && end = "JFK" }

and then found a satisfying instance with Alloy.

Alloy worked great for this example with 6 legs. Beyond the graphical and tabular output, it will interactively allow you to click through to see all possible solutions.

Unfortunately, Alloy runs out of memory on problems well before the 10,000 leg data set, and it’s not clear to me how to change my program to avoid this. (Which isn’t a knock against Alloy — the value of something like Alloy is that it lets you think about your problems at a very high level, keeping you from getting lost in the weeds thinking about things like data structures.)

In the 6-leg example, the solver log output:

19440 vars. 545 primary vars. 47792 clauses. 262ms.

and it certainly feels like 19,440 vars is more than the problem actually has. Perhaps things would be faster if the constraints could be rewritten without Alloy “sequences” (which are just sugar for an Int -> T relation)?

Future work

It’s fun to keep just-complicated-enough problems like this in my back pocket, since they make for worthwhile exercises to try out different languages/techniques.

Some things I’d like to try: