Workshop thermal modeling

← Back to workshop series indexPublished: 2016 November 29

In the high-level workshop envelope overview, I decided to build an unconditioned structure. But just because I’m not actively heating or cooling the workshop doesn’t mean it has to be uncomfortable.

There are lots of architectural strategies for passive heating and cooling (see Sun, Wind, and Light for a great overview). The biggest ones I investigated were:

• insulation
• thermal mass
• solar gain
• air exchange

Unfortunately, most of the information that turned up in my Google searches was frustratingly qualitative. Plenty of Internet commenters sang the praises of garage insulation renovations and sun room porches, but I was interested in tradeoffs:

• Windows have terrible insulation values, but provide free heat from the sun. So will I be warmer with a few windows and lots of insulation or the reverse? (From personal experience, I’ve seen more greenhouses made of glass than Styrofoam…)

• Just how much warm air does it take to warm up a cold concrete slab? With a stiff breeze, will this take 10 minutes or 2 hours?

• Will a large overhead door effectively negate the insulation on the rest of its wall?

I Googled for an embarrassingly long time to try to answer these questions before I remembered that I have a physics degree.

Street fighting mathematics

Of course, a physics degree doesn’t make me a building science expert. But I’m not trying to do exact modeling — just trying to get a feel for the quantities involved.

All models are wrong, and the benefit of making your own model is that you know it’s bullshit (compared to “energy savings” online calculators and magic ASHRAE numbers, where the bullshit is hidden).

In my model, heat moves through the walls via conduction and constantly leaking air. Heat also enters through the windows during the day:

The green parameters are the ones we’ll vary to model different workshop designs, and the workshop’s interior temperature, Tin(t), is the quantity we’re ultimately interested in. It’s related to the total heat within the workshop, Q(t), via the workshop’s heat capacity, hc.

Lots of problems with this model:

• In the model, windows only add heat, but in reality workshop heat probably also radiates out through windows.
• There’s no gravity, and thus no attempt to model convective air flow
• The model ignores humidity, even though water’s latent heat capacity affects the temperature (If you’re naming your metal band, try “Enthalpy of vaporization”.)

If I were trying to get published, I’d call this something like “first order differential model of an isotropic, homogeneous building system with exogenous radiative correction”, but since this is just for my own personal giggles, we’ll call the model “good enough”.

The goal of the model is to inform which passive interventions will affect my personal comfort via the workshop temperature. (Again, since I won’t be conditioning the shop there’s no dollar savings from reduced electric bill or fuel usage.)

So if some strategy costs $5k and moves the “it’s too hot to think in here” peak temperature from 11 a.m. to 5 p.m., I’m happy to pay it. But if that strategy just buys me 30 minutes, it’s not worth it.

Lets look these different terms — conduction, heat capacity, solar gain, and air exchange — to evaluate strategies that could make the workshop more comfy.

Workshop overview

I’m modeling the workshop as a rectangular building: 60’ wide × 20’ deep, with a 3:12 shed roof (15’ on the South wall, 10’ on the North wall), with a 4" concrete slab for half the floor, and wood for the overhanging half. Siding materials are TBD, but I would like some clerestory windows on south wall to bring in daylight. Here’s a rough rendering:

Site temperature

The model’s independent term, Tout(t), is the outside temperature. To measure the daily temperature variation on the site, I left a $40 pen-sized temperature/humidity logger in a shaded location for the month of September. I set it to monitor at five minute intervals, which yielded the resulting temperature data (hour 0 is midnight, September 1):

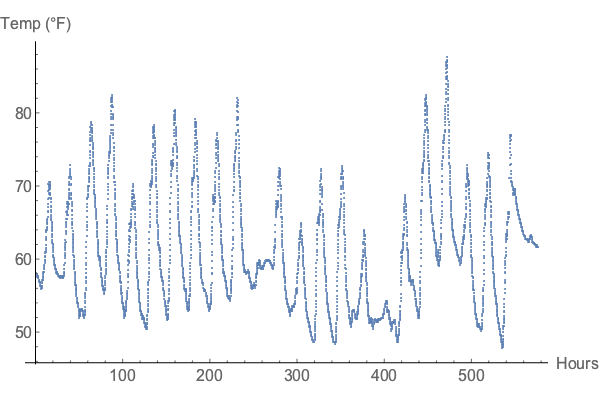
(Aside: Most of the data graphics in this article are real ugly. Partly that’s because I haven’t used Mathematica since college, but mainly it’s because the insanely complex “sometimes expressions are evaluated, but only sometimes” semantics drove me to drink heavily throughout these calculations.)

Two things to note about the site temperature:

1. While it’s hard to see in this graphic, the daily temperature tends to peak around 3:00 in the afternoon.
2. The largest daily temperature swings are about 25°F, and this WeatherSpark graphic suggests that there aren’t larger daily swings in other seasons:

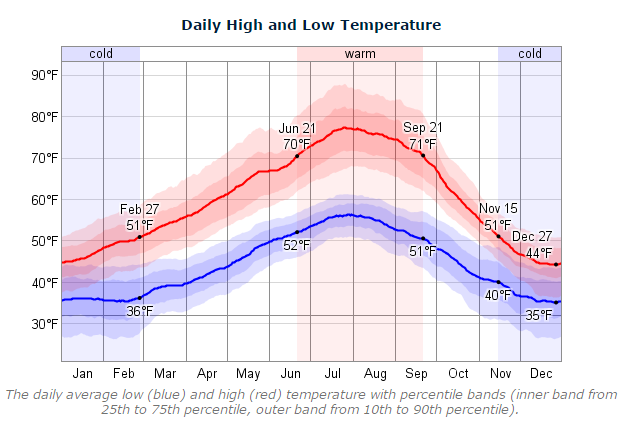
So lets explore passive strategies to modulate the daily temperature swing — ideally reducing the variation so that the workshop is a constant, comfortable temperature throughout the day and night.

Conduction / insulation

A popular strategy to control temperature is to reduce conductive heat flow with insulation.

The ideal insulation is a vacuum, but since that tends to be expensive and has a tendency to violently implode (ever drop a beverage thermos?), typical buildings are insulated with fluffy, air-filled materials like fiberglass (fluffy glass), mineral wool (fluffy rocks), cellulose (fluffy trees), and foam (sort-of-fluffy petroleum).

Mathematically, heat conduction is analogous to electrical conduction: The “voltage” is the temperature difference and the “resistance” is the insulative R-value.

High R-value materials transfer less heat through conduction than low R-value materials.

This leads to the first question: How much insulation (R-value) do I need?

We can ballpark answers by numerically solving the differential heat flow equations I showed earlier. Here are solutions for a 4 day period:

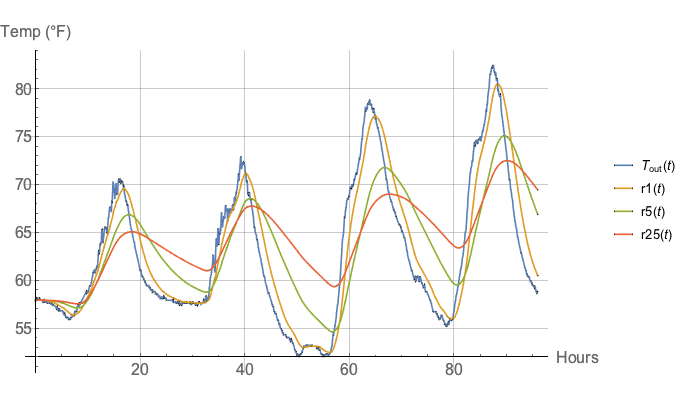
This graphic shows two notable things:

1. There are diminishing returns for increased R-values, with the temperature differences between an R-1 workshop and R-5 workshop much larger than between R-5 and R-25.

2. The difference between the uninsulated (R-1) and sorta insulated (R-5) workshops is about 5°F at most, with the extra insulation moving the daily peak temperature about 90 minutes later.

A higher R-value is always better, but in reality we need to consider the tradeoffs — namely cost. This raises our next question: What’s an achievable, cost-effective R-value?

To answer this question, we should first note that the R-value of a wall assembly tends to be much less than the R-value of the insulation. This is because walls consist of multiple materials, each with its own R-value. The R-value of a glass window, for example, is much less than that of the wood-and-fluffy-insulation part of a wall.

In my case, daylight is a high priority — I’d rather work in a too-cold or too-warm daylit space than in a windowless box. So if I daylight my workshop via clerestory windows in the South wall, what happens to the effective R-value of the wall?

Here’s the analytical equation that gives the effective R-value of a 15’ wall for a given non-window insulation level and polycarbonate window (R-1) height:

(This is the same calculation as the “effective impedance” of parallel electrical resistors, but with relative weighting by area of the wall and window.)

Since I’m not good at abstract, analytical reasoning, I rendered the following contours of the effective R-value:

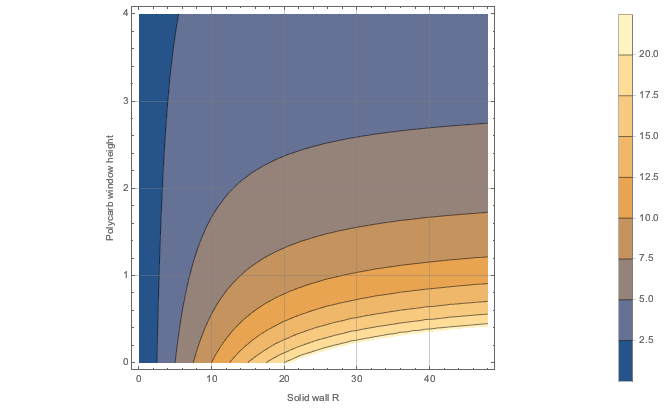
This graphic shows that with 2’ or more of polycarbonate window, the best we can do with the wall is around R-5. Even if we go nuts insulating the solid wall, heat will just move through the R-1 polycarbonate windows.

(The ordinate domain was chosen according to Lawrence Berkeley National Laboratory’s Tips for Daylighting guide, which suggested that 1–4’ of window would provide sufficient daylight.)

In terms of dollars, Home Depot quoted me $2.08/sqft for R-12 sheets of Roxul Comfortboard (fluffy rock), so it’d cost about $2k to bring the South wall from a baseline R-1 to about R-5. (I’m assuming that the other walls, floor, and roof, are similar, so it’d cost something like $10k to bring the entire workshop up to R-5.)

Looking back at our ballpark solution, this means I’d have to spend $10k to reduce the temperature by 5°F and move the peak 90 minutes later.

That doesn’t seem particularly compelling to me — is it the best we can do? Lets look at other strategies.

Air exchange

In my simple model, the heat flow due to air exchange is modeled as a constant rate exchange between the workshop’s interior air and exterior air.

The air exchange rate can be reduced during construction (by sealing envelope cracks with expanding foam, taping sheathing joints, etc.) but is not generally something that can be greatly reduced in a cost effective way.

For the purposes of my modeling, I set the rate to be 1 workshop volume of air exchanged every hour, which corresponds to 260 BTU lost/gained for every °F difference between the inside and outside air.

Solar gain

The sun provides free heat, and in the winter we can capture it to warm the workshop.

Rather to model solar gain from first principles, I took the hourly cumulative values provided by an online calculator, fit a piecewise linear model (connected the dots), and took the derivative to get the solar flux.

Assuming the polycarbonate clerestory windows have a solar heat gain coefficient (SHGC) of 0.8, they’ll pick up about 300 BTU / sqft day over the winter months.

Relative heat flows

Since we have three heat flow terms — conduction, air exchange, and solar gain — it’s worth looking at their relative magnitudes. For the uninsulated (R-1) workshop:

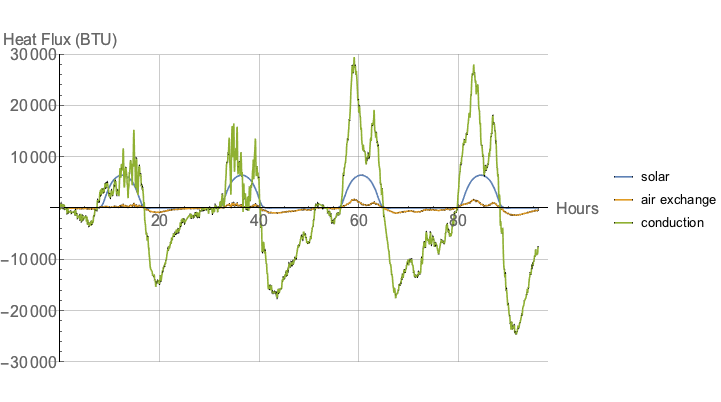
the conduction flow dominates. However, in the insulated (R-5) workshop:

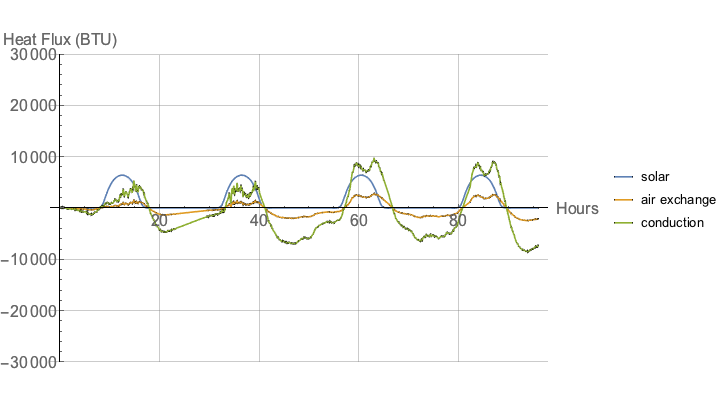
The solar gain and air exchange terms start to matter, though the conduction still dominates.

Given that this is the smallest we can reduce the conduction term, we should explore alternative approaches to regulating temperature.

Thermal mass

Thus far, we’ve explored regulating temperature by reducing heat flows. But we can also regulate temperature by increasing the heat necessary to change the temperature — by increasing the thermal mass (specific heat capacity) of the workshop.

In theory, a large thermal mass will “even out” the temperature: A cold mass will warm up over the day (keeping the workshop cool) and cool off at night (keeping the workshop warm).

Most of the workshop’s thermal mass is provided by the concrete slab and retaining walls. The heat capacity of concrete is about 31 BTU per cubic foot °F.

So my 30’ long × 20’ wide × 4" thick slab requires about 6k BTU to move 1°F. (For comparison, the interior volume of air in the workshop requires only 260 BTU to move 1°F.)

As it so happens, my property has a low-flow well, so if I ever want to live there, I’d be legally required to have a 1000 gallon water reservoir. This reservoir would have a heat capacity of about 8k BTU/1°F, so putting it inside the workshop would double the workshop’s heat capacity.

Lets see what that looks like:

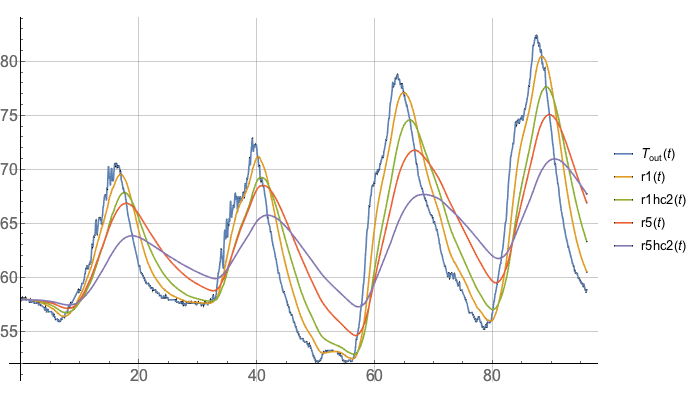
In an uninsulated (R-1) condition, the double heat capacity workshop has a peak temperature about an hour later and 2°F cooler than the baseline slab heat capacity workshop.

In the insulated (R-5) condition, the temperature moderation is more pronounced, with the double heat capacity workshop consistently 3–4°F cooler than the baseline slab heat capacity workshop.

In terms of cost, doubling the thermal mass is effectively free (I have to put that 1000 gallon reservoir somewhere). However, without insulation it doesn’t seem like doubling the heat capacity will meaningfully affect the workshop comfort level.

Conclusion

So, where does all this analysis leave us?

Well, the heat flows are dominated by conduction, which could be reduced with at most R-5 effective insulation for $10k. This insulation, combined with the heat capacity of a concrete slab and 1000 gallon water tank, would reduce peak summer temperatures by 5–10°F at best, depending on the daily swing.

To me, this isn’t worth it. The money could be better spent in several ways:

Interior office: Rather than insulate the whole workshop, I can build an insulated office within the larger workshop envelope. The office would be cheaper to insulate both because it’s smaller, and also because it could use batt or loose-fill insulation in a “double stud wall” configuration rather than the more expensive rigid insulation required by the workshop walls. This office would also satisfy other workshop goals: quiet place from which to operate CNC machine, dust-free place for sensitive equipment and electronics work, etc.

Fancy PPE: If personal thermal comfort does become an issue in the larger workshop, I can buy adorably-named Veskimo cooling vests and $250 battery-powered hand warming gloves and still come out $8k ahead.

Moar tools: I’m a guy who’s building a workshop before his house — given the choice between 5°F of comfort or a sweet Austrian sliding format table saw, what do you think I’m going to pick?

Thanks

Thanks to Matt Sottile and Kovas Boguta for helping me get back up to speed with Mathematica.