← Back to Kevin's newslettersPublished: 2021 Feb 6

It was lovely to hear from everyone who wrote about important work over the last month, thank you! We’ll discuss that weighty topic again, but today let’s play with some technical puzzles.

“Puzzle” perhaps isn’t the best word; I’ve never sought out pure logic puzzles (“the tea drinker lives next to the zebra owner”), wordplay, or arithmetic feats.

Rather, because I’m always making stuff, the technical challenges find me.

My favorite challenges are best described as “things you’d expect a computer to be good at, but only if you’ve never actually used a computer”. These problems are well-posed — there’s obviously enough given data to solve for the unknowns — but in practice turn out to be exceedingly tedious or difficult.

Leaning into this difficulty almost always yields some insight, either about the problem itself (a non-obvious reason why it’s hard) or about some intellectual need which could inspire a new concept or tool.

Today let’s lean into two such problems. For both, I’m curious about:

  1. How you’d actually solve the problem. Not, “I read a cool paper about a technique that might work here”, but what steps you would actually do if someone offered you, e.g., $10k to find the solution in 2 hours. How confident are you that you’d even be able to do it?

  2. If you couldn’t solve it, what tools/concepts would build if you had a month (or year!) to prepare?

I’m genuinely curious about both questions — please reply and I’ll share next time the empirical state of the art (as known to this newsletter’s handsome, above-average-intelligence practitioner demographic).

Geometry

The first one is a simple geometry problem. Here’s a bitmap drawing of a module that I’d like to solder to a circuit board that I’m designing:

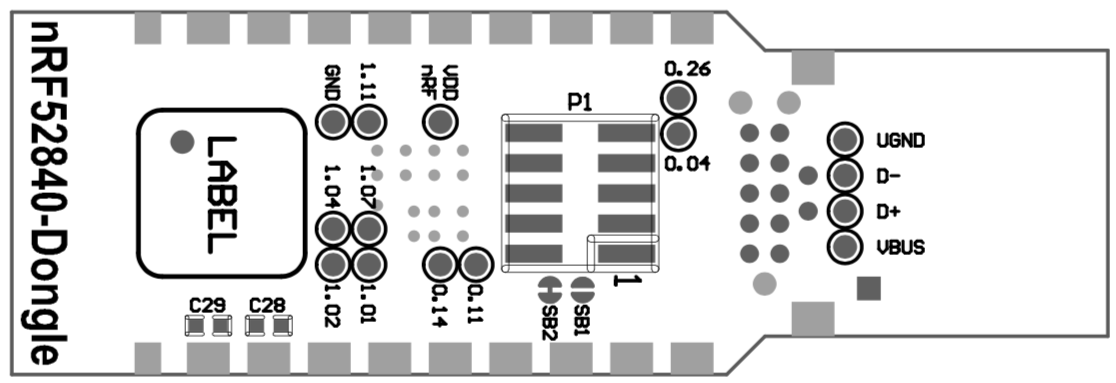
nrf52840 dongle assembly drawing

I need to put matching pads on my board, so I need to know the physical sizes and offsets (measured from centers, in millimeters) of the rectangles (in rows along top/bottom edges) and labeled circles (in the field).

I know (because I have calipers) the module is 15.24mm wide, and let’s call the bottom left corner the origin.

Obviously this problem can be solved — the information is all there in the picture — but how would you solve it?

Could you do it in under 5 minutes?

I am ashamed to admit that, even with a degree in physics and more than a decade in professional computing, this problem took me an hour (and if I “solved” it again, I’d probably get slightly different answers).

I asked on Twitter, but as of this writing only one person had a better solution than “uh, trace it in Illustrator I guess?”

Resistor combinatorics

Also from the “gosh, he’s still making keyboards isn’t he?” department, I recently needed a non-standard resistance value for a wireless charging coil design.

While my favorite PCB assembly service is inexpensive, high-quality, and fast, they stock only about 3000 resistors. (It’s fast and cheap because they only assemble from a limited selection of parts that they keep loaded on assembly line robots.)

Luckily, resistors cost less than $0.01 each and can be combined according to simple rules, so it’s fine to use as many as we need. E.g., a needed 77 Ohm resistance can be made by wiring up 60 + 10 + 5 + 2 Ohm resistors in series. (Similarly, resistors can be “reduced” by combining them in parallel; two 10 Ohm resistors in parallel yields (1/10 + 1/10)-1 = 5 Ohms.)

Consider the simplest case: From a catalog of 3000 resistors, how would you select two to combine (in series or parallel) to best approximate a target resistance R?

The two-resistor case is easily brute forced (107 possibilities), but you’ll need to get clever to find solutions with, say, 10 resistors.

Rather than get clever by writing my own search/sort algorithm (encoding pruning heuristics like “For target resistance R, don’t bother looking at resistances > R”), I figured that an established solver like Z3 would do much better than anything I could write myself.

Unfortunately Z3 gave up trying to select two resistors from a library of just 2000 (my source code). (I didn’t try MiniZinc or any of its backing solvers, as they struggled with a similarly simple small problem last I tried them.)

Do I have unreasonable expectations for what I (an amateur) should be able to accomplish with an off-the-shelf solver in 2 hours? Or did I just get unlucky?

Is there a Mathematica or NumPy one-liner I missed here? Or is solving this problem for a network of 10-resistors drawn from 3000 component values a PhD-level project?

I’m aware that adding constraints often makes a problem more tractable for a solver (by reducing the search space), but shouldn’t a solver be able to brute force a search space of just 30002 possibilities?

How would you solve this? (CSV of resistor values in this gist.)

Unsatisfied with satisficing

I don’t think either of these problems are really that difficult. At least, passable solutions can be generated by pouring a stiff drink and sitting down for an hour to trace in illustrator or construct by hand resistor networks.

But every time we catch ourselves performing rote intellectual labor on a computer is a chance to really introspect and understand how and why our tools have let us down.

If we don’t do that, how can we improve things?

I’m looking forward to hearing what y'all think — let me know if you’ve got good solutions to these two problems, or if you’ve any favorite “really, it seems like computers should be able to do this…”-type challenges.

Misc. things